昨日介紹了使用多項式商環建構了高維度的（2N 維度）的晶格密碼系統，今日我們來簡單討論相關的高維度晶格攻擊方法：

基底化約演算法

我們在 Day4 時破解了二維晶格密碼學，當時所使用的技術叫做「高斯化約（Gauss reduction）」。這個演算法的關鍵在於：給定一組基底 v1, v2 ，我們想辦法把 v1 減去 v2 的整數倍，好讓其結果與 v2 儘量垂直，接著把 v2 減去 v1 的整數倍，好讓其結果與 v1 儘量垂直，以此步驟循環的做下去。最後可以得到比原本的 v1, v2 還要短很多的基底，取其中一個拿去解密通常可以成功（詳細理由請回顧 Day4）

連續空間中的基底化約

現在當然就可以推廣類似的想法到高維度晶格。如果你有學過線性代數裡面的內積、正交基底，那你一定聽過 Gram-Schmidt Orthogonalization 。這個演算法本質上就是接受一個（壞）基底 v1, v2, ..., vn ，然後計算輸出一個（好）基底 v1*, v2*, ..., vn* 。

在這個計算當中，第一步會令 v1* = v1。
接著因為 v2 向量可以分解成與 v1* 垂直的部分以及與 v1* 平行的部分，所以將 v2 扣掉與 v1 平行的部分（即只剩下與 v1 垂直的部分），當作 v2*

接著，v3 向量可以分解成與 v1*, v2* 垂直的部分以及「其他部分」，當我們把「其他部分」從 v3 扣掉後，就剩下與 v1*, v2* 垂直的部分，把這個當作 v3*

以此類推，vk 向量可以分解成與 v1*, v2*, ... vk-1* 垂直的部分以及「其他部分」，當我們把「其他部分」從 vk 扣掉後，就剩下與 v1*, v2*, ... vk-1* 垂直的部分，把這個當作 vk*。

做完後，我們就可以得到一組新的兩兩向量都互相垂直的基底。

晶格基底化約

可惜上面這個方法無法直接在晶格裡面使用：如果仿造這樣的做法，步驟會變成

第一步令 v1* = v1
接著我們從 v2 扣掉 m 倍的 v1*，記為 v2*。但因為我們在晶格，只能扣去整數倍的向量，所以我們只能找一個還算可以的整數 m ，盡量讓 v2* = v2 - m v1* 與 v1* 垂直。

到了第k-1步驟時， vk 向量可以減去 v1*, v2*, ... vk-1* 的整係數線性組合

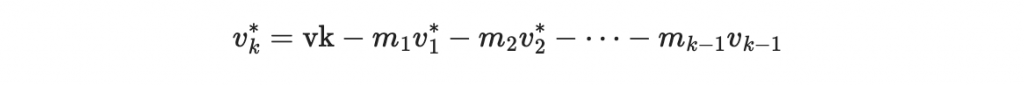
其中我們要盡量選擇整係數 m1,..., mk-1 好讓 vk* 盡量與 v1*, v2*, ... vk-1* 皆垂直。

做完後，就可以得到一組新的好基底 v1*, v2*, ... vn* 。

詳細的步驟請參見 ref.

安全性

雖然我們剛講完一種基底化約攻擊方式，但是也不必太過擔心。密碼學家不斷在使用數學方法分析。只要在維度很大的時候，這樣的基底化約攻擊仍然很難找到足夠短的短向量。這個維度的數字大約落在六百維的到兩千維，這也是實作上能看到的晶格結構。

晶格密碼學之我見

好的！今天是鐵人賽的第九天，我們已經花了快要三分之一的時間來講「晶格密碼學」。

晶格密碼學可說是後量子密碼學各大家族中相對比較直得期待的一族。密鑰長度適中、加解密演算法都有許多優化與library支援（而我本人也正在做相關的開發）、目前也未見安全性上有重大威脅，不論對量子電腦或是對傳統電腦來說。

NIST 所通過的標準草案

美國標準，那幾乎就是世界標準

目前使用晶格密碼系統的有三個演算法：

加密：
Kyber

簽章：
Dilithium
Falcon

這些真正在使用的密碼系統，雖說都是建立在晶格的概念上，但是相關的數學細節非常複雜。我們只能先退而求其次，把 NTRU 吾乃數論學家 好好先講清楚。（NTRU 中的晶格結構，那些多項式環，其實也有被 Falcon 所採用，倒也不是完全無關）

待我完成30天挑戰賽後，未來有機會的話，我們再用中文專題介紹以上三種超複雜協議（喔尤其那個 Falcon 又是晶格又是傅立葉滿天飛（？））

明天開始，我們會開始講下一個主題，「多元二次方程組密碼系統」。

ref:

NGUYEN, Phong Q.; VALLÉE, Brigitte. The LLL algorithm. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010.